Trinomial (a = 1) Factorization
If you are stuggling with factoring quadratic trinomials of the form x2+bx+cx2 + bx + cx2+bx+c? Well, help is here! Our Free Factoring Calculator will make this task easier for you! You can enter your quadratic expression, with the coefficient of x2x2×2 being 1, and get the result instantly.
This tool will absolutely come in handy to students, teachers, or anyone checking algebra homework involving equations and expressions.
What is a Trinomial?
in simple words, a trinomial is defined as a polynomial that has three terms.
Its general form is:
ax^2 + bx + cax^2
Here:
a is the coefficient of x² (quadratic term)
b is the coefficient of x (the Linear Term)
c is the constant term of the polynomial
Constant Term of a Polynomial
When a = 1, it becomes easier to work with this, since now the formula begins with x², not a numeral times x².
So our equation is this:
x2+bx+cx2+bx+c
This is called Trinomial, where a = 1, the easiest form of the quadratic to factor.
Why Factorization Matters
Removing one element from one of the three parts of a trinomial expression doesn’t really help us simplify it any further.
This is what partial factoring looks like:
x^2 + 5x + 6
= x^2 + 5x + 6
= 2x + 6 + 3x
= 2(x + 3) + 3x
= 2(x + 3) + 3(x + 2)
The simplification process is more about how to describe more complicated expressions.
- Simplifying Equations
- Forming Quadratic Equations That Have Quadratic Solutions
- Solving Quadratic Equations That Are Part of Real Life Situations (e.g., areas, motion, and other optimizations)
Factoring an expression is like removing a number from a set of number and its factors a prime.
Using a Trinomial (a = 1) Factorization Calculator
Doing factorization manually is great for learning, but when working with large numbers or decimals, it’s easier to use a Calculator.
This smart tool automatically:
Identifies b and c
Calculates the correct factor pair (m and n)
Displays step-by-step factorization
Gives you the final product (x + m)(x + n) instantly
Example:
Input: x² + 11x + 24
Calculator Output: (x + 3)(x + 8)
It’s fast, accurate, and helps students, teachers, and professionals save time while learning the method properly.
The Trinomial (a = 1) Formula
For trinomials where the leading coefficient is 1, the goal is to find two numbers (m and n) that satisfy two conditions:
- Their product equals the constant term (c)
- Their sum equals the coefficient of x (b)
In other words:
m×n=cm × n = cm×n=c m+n=bm + n = bm+n=b
Once you find m and n, you can express as:
x2+bx+c=(x+m)(x+n)x^2 + bx + c = (x + m)(x + n)x2+bx+c=(x+m)(x+n)
Step-by-Step Process
Let’s break it down clearly:
- Write down: x² + bx + c
- Identify b and c (the coefficients)
- Find two numbers that multiply to c and add to b
- Write them inside binomials (x + m)(x + n)
- Check to verify the answer

Example 1: Factor x² + 5x + 6
b = 5, c = 6
Find two numbers that multiply to 6 and add to 5 → 2 and 3
Substitute: (x + 2)(x + 3)
Answer: (x + 2)(x + 3)
Check:
(x+2)(x+3)=x2+3x+2x+6=x2+5x+6(x + 2)(x + 3) = x^2 + 3x + 2x + 6 = x^2 + 5x + 6(x+2)(x+3)=x2+3x+2x+6=x2+5x+6
Example 2: Factor x² + 7x + 12
b = 7, c = 12
Numbers that multiply to 12 and add to 7 → 3 and 4
So:
x2+7x+12=(x+3)(x+4)x^2 + 7x + 12 = (x + 3)(x + 4)x2+7x+12=(x+3)(x+4)
Answer: (x + 3)(x + 4)
Example 3: Factor x² + 2x – 8
b = 2, c = -8
Need two numbers that multiply to -8 and add to 2 → 4 and -2
So:
x2+2x−8=(x+4)(x−2)x^2 + 2x – 8 = (x + 4)(x – 2)x2+2x−8=(x+4)(x−2)
Answer: (x + 4)(x – 2)
Why Learning Trinomial (a = 1) Factoring Is Important
This technique might seem simple, but it’s the foundation of higher-level algebra.
Here’s why it’s so valuable:
Helps Solve Quadratic Equations:
You can find the roots (x-values) easily by setting each factor to 0.
Simplifies Complex Expressions:
Makes equations easier to handle and understand.
Used in Real-World Problems:
Like physics (motion), geometry (area), and engineering (design equations).
Prepares You for Advanced Factoring:
Such as General Trinomials (a ≠ 1) and Quadratic Formula methods.
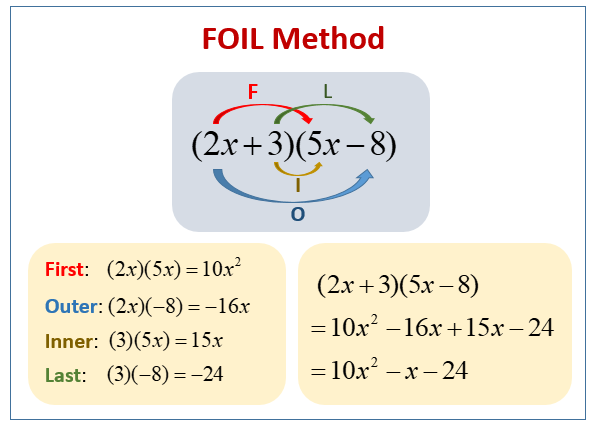
How to Verify Your Answer
After factoring, you can double-check your work using the FOIL (First, Outer, Inner, Last) method.Example:
(x+4)(x−2)(x + 4)(x – 2)(x+4)(x−2)
First: x × x = x²
Outer: x × (-2) = -2x
Inner: 4 × x = 4x
Last: 4 × (-2) = -8
Combine:
x² + 2x – 8
If you get the original answer, your factorization is correct!
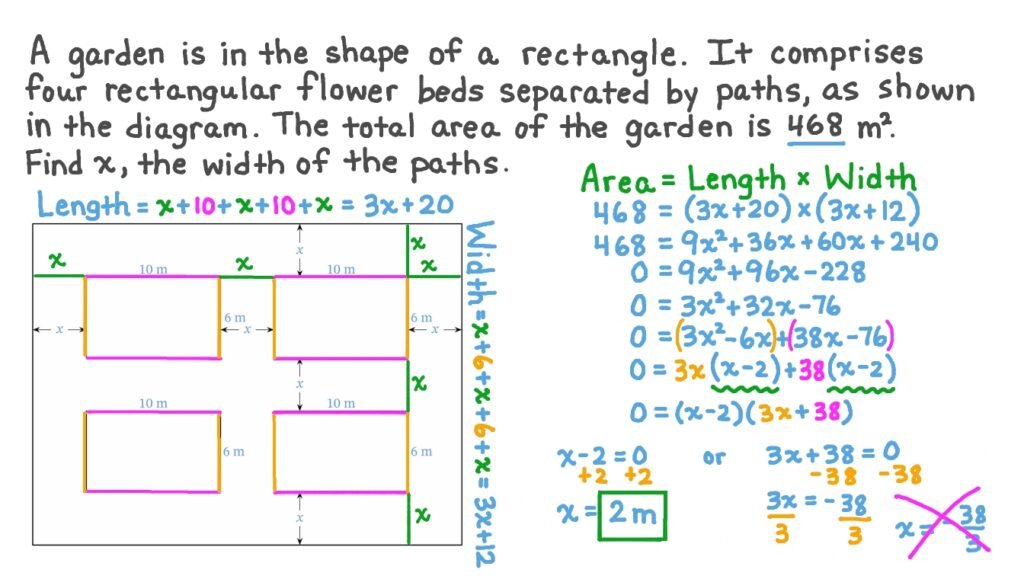
Real-Life Example
Imagine designing a rectangular garden where the area (A) is given by:
A=x2+5x+6A = x^2 + 5x + 6A=x2+5x+6
Factoring gives:
A=(x+2)(x+3)A = (x + 2)(x + 3)A=(x+2)(x+3)
Now, it’s easy to see that if one side is (x + 2) meters, the other is (x + 3) meters.
This helps visualize dimensions and relationships something algebra enables beautifully.
Common Mistakes to Avoid
- Sign Errors:
Forgetting whether the constant is positive or negative often leads to the wrong pair. - Wrong Number Pairs:
Some students pick numbers that multiply correctly but don’t add to b. Always check both rules. - Not Checking Work:
Skipping the verification step can hide small mistakes. - Assuming a ≠ 1:
This formula works only when the first coefficient is 1. For other cases, you’ll need the General Method.
Conclusion
Factoring a (a = 1) may seem basic, but it’s a powerful algebraic tool that simplifies equations and reveals the hidden structure behind mathematical expressions.
The process is simple:
- Identify b and c
- Find two numbers that multiply to c and add to b
- Write the expression as (x + m)(x + n)
Whether you’re solving problems manually or using a calculator, mastering this concept makes algebra intuitive and logical. Once you’re comfortable with a = 1, you’ll be ready to tackle more advanced ones where a ≠ 1, which we’ll explore next.
